2021年11月6-7日，由兰州大学哲学社会学院与中国自然辩证法研究会数学哲学专业委员会联合主办，兰州大学哲学社会学院与《科学·经济·社会》杂志社承办的“2021年全国数学哲学学术研讨会”顺利举行。由于疫情原因，会议改为线上举办，来自全国20余所高校、研究机构的50余位专家学者参加了本次会议。

 

第一节

开幕式由山西大学副教授康仕慧主持，兰州大学哲学社会学院院长陈声柏出席开幕式并致辞，数学哲学专业委员会秘书长杨睿之宣布了新一届委员会名单。陈声柏教授结合自身的求学经历与教学经历，回顾了兰大哲学社会学院逻辑学科的发展。他特别强调了哲学与逻辑、自然科学的紧密关系，展望了兰大相关学科的未来发展，并祝愿研讨会顺利举行。陈声柏教授真诚、殷切的致辞让与会学者倍感暖心。

 

 

首日的报告分为上下午两场，上午为三场大会报告。首场报告由北京交通大学宋诗畅副教授主持，南开大学丁龙云教授做了题为《等价关系与波莱尔归约》的报告。

丁教授认为，数学各分支的结果和问题之间进行比较是逻辑各不同分支研究问题的共同方式。等价关系就是其中的一种方法。通过代数和拓扑中的四个例子，某个等价关系可以通过归约转换成另一种等价关系，数学中很多定理符合归约这种抽象形式。我们又希望归约映射携带一些有价值的信息，这就引到了Borel归约。丁老师回顾了Polish空间、Borel分层、Borel函数等概念，引入了Borel归约的定义。通过泛函分析里一个定理重新解释到Borel归约框架中，说明了Borel归约的重要价值。通过这些背景的介绍，丁老师后面又引入了smooth的等价关系、\pi_1的等价关系、可数等价关系、解析等价关系等，为大家展示了一些前沿的结果，例如二分定理。

 

 

第二场大会报告由清华大学俞珺华副教授主持。华南师范大学熊明教授带来了题目为《Solovay functions and paradoxes》的报告。报告介绍了与哥德尔不完全性定理类似的Solovay算术完全性定理：GL可被用于刻画PA的可证性。它可以被看作某些不完全性定理的大概括。聚焦它的证明，与哥德尔定理类似，需要使用对角线引理构造不可判定的语句。哥德尔对角线的构造与说谎者语句（悖论）相关，由此引出报告的主要问题：Solovay对角线构造的可能思想启发是什么？可能是一种悖论吗？熊老师为大家介绍了真理论的一些内容、形象地用难民为例介绍了Solovay函数并澄清了什么是“悖论的”。借此“框架”，熊老师向我们展示了如何得到特定模态逻辑框架下的Solovay-说谎者语句，以及这些语句的基本性质。因此，我们能将Solovay的构造与常规的自指语句进行混合，得到一些比通常说谎者悖论严格更弱的悖论。

 

 

第三场大会报告由中山大学珠海分校王轶副教授主持。北京大学王彦晶副教授带来了题目《What is intuitionistic truth》的报告。王老师首先强调了理解直觉主义逻辑和直觉主义真的必要性。他从自己对直觉主义逻辑的困惑讲起，介绍了直觉主义逻辑的早期技术和现在的一些应用。例如，在数学、计算机和哲学中都有直觉主义逻辑的应用。但现在的趋势是，仅通过直觉主义逻辑得到一些技术性的结论，但直觉主义逻辑这个概念背后的本质仍然是不太清楚的。在这个背景下，介绍了Brouwer-Heyting-Kolmogorov对proof的解释，但proof不足以得到直觉主义的真。传统上，我们将直觉主义的真等同于可证。但对不同背景的人群，可证是一个不尽相同的概念，因此不是一个对直觉主义真的足够好的解释。王老师从历史、哲学和模态逻辑多个角度讨论了如何理解直觉主义逻辑：Kolmogorov对直觉主义逻辑的理解、Medvedev逻辑及其基本思想在多领域的发展，可观察到其背后的思想和认知逻辑之中的哲学讨论十分类似，但直觉主义的真可能和知识仍有很多不同。又讨论了Heyting、Martin-Lof、Hintikka、Van Benthem等人对直觉主义逻辑的理解。据此，报告给出了直觉主义逻辑语义的一种模态逻辑定义，并讨论了这套对直觉主义逻辑真理解的诸多意义。

 

 

第二节

下午场的报告由首都师范大学教授叶峰主持。第一场由复旦大学副教授杨睿之 带来题目为《形式主义与多宇宙观》的报告。杨老师从希尔伯特纲领的原初形式主义讲起，形式主义近年来借助其他形式，例如集合论多宇宙观，重新复活。在数学家、计算机学家中，形式主义仍得到了广泛的同情，尽管原初形式的形式主义希望渺茫。因此，改良的形式主义在今天的数学哲学讨论中仍有出现，形式主义据此复活。例如可取消的结构主义。一些学者论证集合论多宇宙观是一种形式主义。本报告的主题是，新形式的形式主义仍面临的困境，多宇宙观有超出形式主义的价值。

      为了实现这一目标，杨老师分析了形式主义的基本立场，分别讨论了以下几种形式主义：希尔伯特的形式主义，它不是本体论中立的，即必须论证为什么有一部分数学是有意义的而另一部分不是；集合论的形式主义，例如Paul Cohen、Shelah等，他们认为谈论独立于ZFC的命题的真假是无意义的，但这也蕴涵着几种分层，ZFC和ZFC之外的、ZFC的后承与独立于ZFC的命题等，这面临和希尔伯特形式主义类似的困难；Curry的形式主义，认为数学是形式系统的科学，直觉主义、柏拉图主义等都可以与之相容，不同的形式系统，只要不是不一致，都是某种程度上可接受的，杨认为这种形式主义仍然是有问题的；Azzouni的形式主义。杨又通过一个简单的集合论事实论证，ZFC可以任意扩张到一个形式系统，使得它们得到一些完全矛盾的结论，据此认为我们必须要超出形式系统的东西对形式系统进行辩护。他简短地陈述了多宇宙观为什么是超出形式主义的。

 

 

第二场由山西大学的高坤老师带来题目为《哥德尔纲领的实现能支持数学实在论吗？》的报告。本报告主要论证哥德尔纲领对实在论的两种论证都是不成立的。一开始，高简要介绍了哥德尔纲领的历史，详细介绍了哥德尔的实在论，哥德尔纲领就是旨在解决集合论独立性问题的一个研究方案，其通行的表述为：合理地扩充ZFC，比如增加大基数公理，最终判定CH的真假。高老师认为，哥德尔纲领是一个相对纯粹的数学研究纲领，它不一定蕴含数学实在论。哥德尔纲领下的数学实践包括加州学派的工作，例如为三阶算术寻找经验完全的理论，寻找一个类似于L的能容纳所有大基数的内模型。这些本质都是数学问题。但即便终极L存在，是否意味着实在论成立？

第一种实在论的论证认为，哥德尔纲领以实在论为假设，如果哥德尔纲领能实现，那么对实在论有确证作用。高老师反驳说，实在论对哥德尔纲领可能并不是必要的。例如，Maddy论证数学在方法论上具有自治性，数学家为一些概念公理等做辩护的理由实际上是来自数学内部的，那些理由不是出于哲学目的；哥德尔本人的一些论述也表明实在论并非不可或缺的，比如迭代概念就足以帮助我们追求新公理，无需实在论。高老师认为，哥德尔纲领的合理性源于集合概念的开放性，即便数学是一种概念想象活动，也可以接受哥德尔纲领。第二种实在论的论证认为，哥德尔纲领的实现印证了ZFC扩张的唯一性，除了柏拉图主义之外寻找不到其它哲学解释。高老师认为就理论的优良性质而言，几何、数论、分析等似乎足以论证数学实在论了；其次，高老师认为哥德尔的外在辩护方法与实在论不相容，例如实在的那个世界完全可能是毫不满足我们的理论偏好。进一步地，高坤认为，子集公理、基础公理就已经与实在论冲突了。

 

 

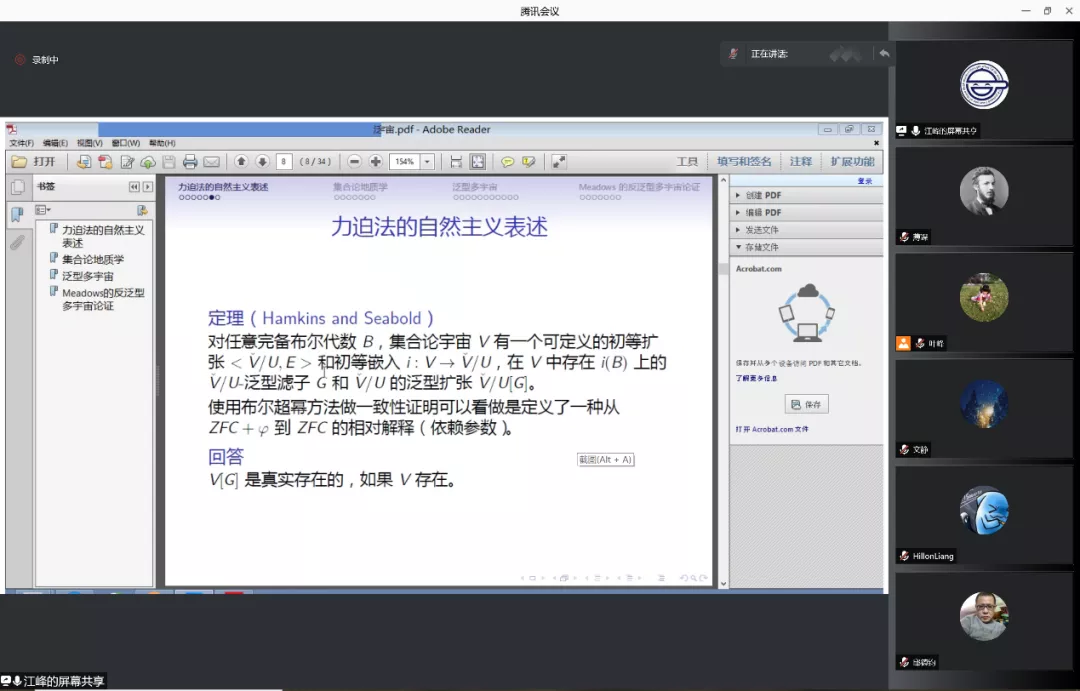
下午的最后一场报告由首都师范大学的硕士生江峰带来《从集合论地质学到泛型多宇宙》这个报告分为三部分，第一部分报告人介绍了Hamkins和Seabold提出的“力迫法的自然主义表述”，相比于通过操作ZFC的足够大的有穷片段的可数传递模型的力迫法的标准表述，这种表述能让我们更直接的谈论集合论宇宙V和V的泛型扩张V[G]，而不必为V-泛型滤子的存在性而困扰。报告人认为，这种力迫法的自然主义表述可以回应许多对V[G]的存在性的质疑，从而说明泛型多宇宙不是一种幻觉。报告的第二部分介绍了集合论地质学中一些新近的结果对泛型多宇宙的基本结构的影响。报告的第三部分分析了Toby Meadows针对泛型多宇宙提出的一个反驳，简单来说，Meadows通过证明Steel的泛型多宇宙理论GMV+\exist W(W=终极L)和ZFC+V=终极L这两个理论非常接近来说明泛型多宇宙是多余的。报告人认为， Meadows的这个技术性结果依赖于一个非常特殊的假设，不能说明泛型多宇宙是多余的。

 

 

第三节

11月7日的报告分为两部分，第一部分由中山大学沈榆平副教授主持。首先，吉林大学的康孝军副教授为大家带来了《从实用主义看反推数学》报告。报告从反推数学的主要问题讲起，反推数学试图讨论数学中证明特别的定理集的时候需要什么样的公理，即从定理“反推”公理。对反推数学中，一般会考察二阶算术的五大基本子系统，报告简单介绍了RCA0能证明的和能证明等价于其它子系统的定理和不能证明的定理。反推数学之源是希尔伯特纲领，尽管原始希尔伯特纲领因为哥德尔的工作失败，但相对化的希尔伯特纲领仍在继续，即数学在基础框架的有效性能在一个更严格或更弱的基础框架中实现。例如predicative math可以被归约到有穷主义数学。反推数学就是这种意义下是希尔伯特纲领的部分实现，并且容易看到，这种希尔伯特纲领具有工具主义倾向。它试图将经典数学解释为有穷主义数学，它的工具标准包括一致性、实用性和简洁性等。反过来，报告介绍了实用主义的几种真理观，并且认为各种数学哲学观点都承认数学具有实用性。基于实用性，反推数学也可以用于寻找新公理、讨论真与可证明的关系等意义，因此其具有实用主义色彩。我们可以基于反推数学，得到一种反推数学版本的实用主义真理观，可以寻找到可修正的数学真理。

 

 

第二场报告为中山大学萧浩健助理教授带来的《点、间隔与含数字句子真值》。报告先从两个问题开始：如何用数学语言描述世界的事情？语言中出现的数字它们更像点还是区间？借助这两个问题，报告介绍了点主义和区间主义的基本观点与它们的区别。紧接着聚焦于点主义，考察了一种“虽然……但是……”句子，发现用点主义的方法用于分析句子会有点奇怪。近期有一些点主义的文献试图解释这种现象，报告详细介绍了“相关原则”修正含数字句子的意义，例如比较句问题。还讨论了它的一些问题和一些区间主义的诘难，例如，点主义可以用一种混合观点来坚持立场。此外，还介绍了一些用语用的角度分析的一些特殊情况的处理。

 

 

第二部分的报告由山西大学的康仕慧副教授主持。第一场报告为复旦大学的博士生寇亮带来的《反映原理作为大基数内在辩护的不可行性》。这个报告从公理辩护的背景讲起，逐步引入哥德尔的内在辩护和外在辩护概念并聚焦于内在辩护。报告人通过分析哥德尔、王浩、P.Koeller、P.Maddy等人的作品，认为内在辩护即是基于集合概念本质的辩护。报告分析了集合概念的本质至少包含三点：非完成性和不可穷尽性、不可定义性以及与序数的本质相关。由此，报告人认为基于反映定理的反映原理是一种内在辩护。紧接着报告分析了几种反映原理：RP2、Reinhardt的反映原理和Welch的GRP它们能为何种形式的大基数公理作出辩护，最终发现这些反映原理或者不能超出L或者是不可靠的，并通过引入原则U说明了为什么反映原理不可靠。

 

 

第二场报告为山西大学的硕士生梁德柱带来的《数学中的无穷——论严格有穷主义及其挑战》。报告从有穷主义的各种形式讲起，聚焦于叶峰的严格有穷主义。严格有穷主义是基于物理主义世界观的一种数学哲学主张。严格有穷主义主张现代科学刻画的世界不支持存在物理宇宙之外的对象。严格有穷主义认为在原则上可以将经典数学的应用过程表达为具体事物的推导，即无穷的数学理论是不必要的。报告从“物理主义世界观”和“必要性”角度提出挑战。介绍了曹天予的结构主义实在论对物理主义世界观的批判，又从模糊逻辑、模糊公理集合论的角度讨论了无穷在数学中是必要的，而不是可消除的。另一个无穷必要性的论证是概率论中的可能性空间假设。针对物理主义认为一致性信念的来源是经验归纳，可应用性或有些经验来源并不能蕴含数学理论为真。据此，报告引入了虚构主义。虚构主义也对无穷概念提出了挑战，他们认为数学是一种约定、虚构，但数学理论的确是正确的、可应用的，因而可以某种程度上兼容无穷概念的同时不介入物理主义世界观。报告认为虚构主义介于物理主义的严格有穷主义和柏拉图主义之间，陈述了一些支持选择虚构主义的理由。

 

 

会议的最后，针对最后一场报告中的虚构主义、物理主义、柏拉图主义中的问题，几位专家展开了激烈的讨论。最后，新一届委员会主任邢滔滔教授对大会做了总结，也对数学哲学未来的发展进行了美好的展望。